Getting Started

Welcome to the rom-comma Python package, which implements Reduction of Order by Marginalization (ROM) via Global Sensitivity Analysis (GSA) using Gaussian Process Regression (GPR). Those unfamiliar with these topics are advised to follow the hyperlinks to the page glossary. This advice applies to much of this user guide – we make extensive use of glossaries.

The mathematics behind this software is covered in some detail in a paper currently under peer review for publication.

Installation

Simply place the romcomma package (or its parent rom-comma) in a folder included in your PYTHONPATH (e.g. site-packages). Test the installation by running the rom-comma installation_test module, from anywhere. Runtime dependencies are documented in pyproject.toml.

Conceptual Hierarchy

The romcomma package is organized in a modular hierarchy

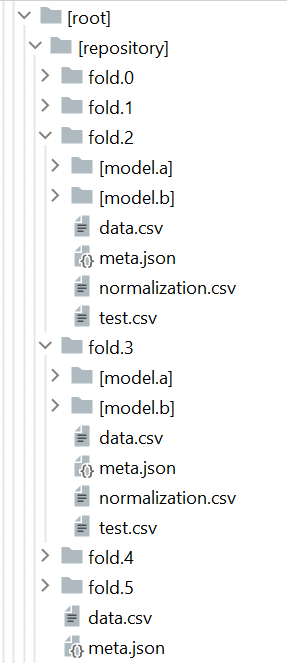
Module Hierarchy

The romcomma package is organized in a modular hierarchy

• romcomma
  • romcomma.base
    • romcomma.base.classes
    • romcomma.base.definitions
  • romcomma.data
    • romcomma.data.storage
  • romcomma.gpf
    • romcomma.gpf.base
    • romcomma.gpf.kernels
    • romcomma.gpf.likelihoods
    • romcomma.gpf.mean_functions
    • romcomma.gpf.models
    • romcomma.gpf.tests
  • romcomma.gpr
    • romcomma.gpr.kernels
    • romcomma.gpr.models
  • romcomma.gsa
    • romcomma.gsa.base
    • romcomma.gsa.calibrators
    • romcomma.gsa.models
  • romcomma.rom
    • romcomma.rom.old
  • romcomma.user
    • romcomma.user.contexts
    • romcomma.user.functions
    • romcomma.user.regression
    • romcomma.user.results
    • romcomma.user.run
    • romcomma.user.sample

No module depends on any module below it in this table. We refer to items in this list as modules, even if they are technically packages.

The romcomma.user module comprises a gallery of archetypal user scripts to cannibalize.

User functionality is for the most part exposed in the penultimate module, romcomma.run. Any direct call to functionality outside romcomma.run may be regarded as bespoke, not to say advanced.

Glossary

package

Python package

module

Python module or package.

GPR

Gaussian Process Regression. A quite general technique for representing a functional dataset as a (Gaussian) stochastic process described thoroughly in [Rasmussen and Williams 2005].

GSA

Global Sensitivity Analysis. This Assesses and ranks the relevance of a system’s inputs to its outputs by a variety of methods covered broadly in [Saltelli et al. 2007] and [Razavi et al. 2021]. rom-comma deals exclusively with the variance based method of Ilya M. Sobol. This has been somewhat extended, as described in gory technical detail in [Milton et al. 2023].

ROM

Reduction of Order by Marginalization. A novel approach to locating an Active Subspace (AS) using conditional variances or Sobol’ indices. In the Active Subspace technique [Constantine 2014] the input basis is rotated to align with the eigenvectors of the squared Jacobian vector. In ROM, the input basis is rotated to maximise the Sobol’ index of the first \(m\) inputs.